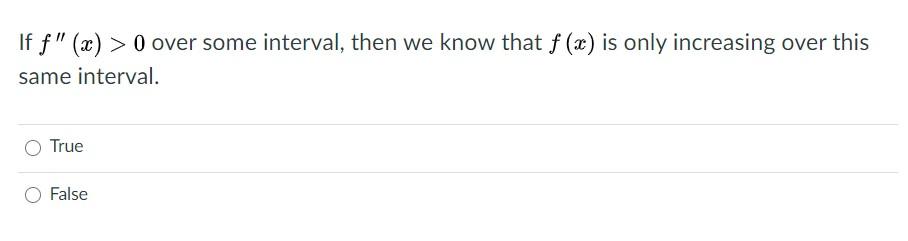
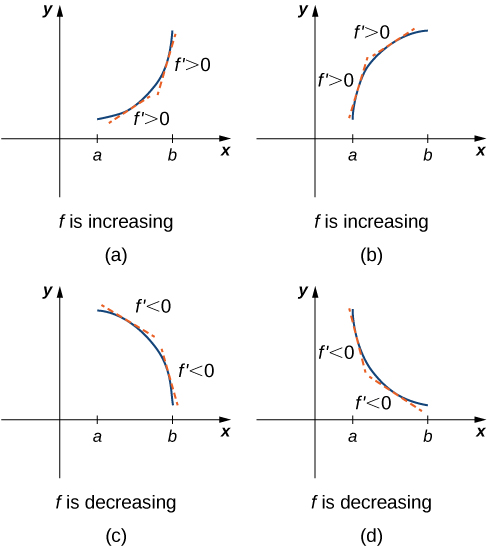
If f′′(x) > 0 on an interval, then f′ is increasing (slopes are becoming bigger), which means f is CONCAVE UP If f′′(x) < 0 on an interval, then f′ is decreasing (slopes are becoming smaller), which means f is CONCAVE DOWN If a function changes concavity at x = a, then f has an INFLECTION POINT at x = a (provided x = a is🔴 Answer 2 🔴 on a question F(x)< 0 over (∞, 3) and what other interval? Correct answers 3 question On a coordinate plane, a curved line with a minimum value of (negative 25, negative 12) and a maximum value of (0, negative 3) crosses the xaxis at (negative 4, 0) and crosses the yaxis at (0, negative 3) Which statement is true about the graphed function?

Which Statement Is True About The Graphed Function F X Lt 0 Over The Intervals 0 7 And Brainly Com
F x 0 over and what other interval
F x 0 over and what other interval- f(x)=xln(x) is concave up on the interval (0,∞) To start off, we must realize that a function f(x) is concave upward when f''(x) is positive To find f'(x), the Product Rule must be used and the derivative of the natural logarithmic function must be known Product Rule (Simplified format of the rule) (Derivative of first)(Second function) (First function)(Derivative of theSimple we make it periodic Consider one possible way of doing this The graph of our original function is 05 10 15 05 10 15 Fig 3 Graph of y = x on (0, 2)
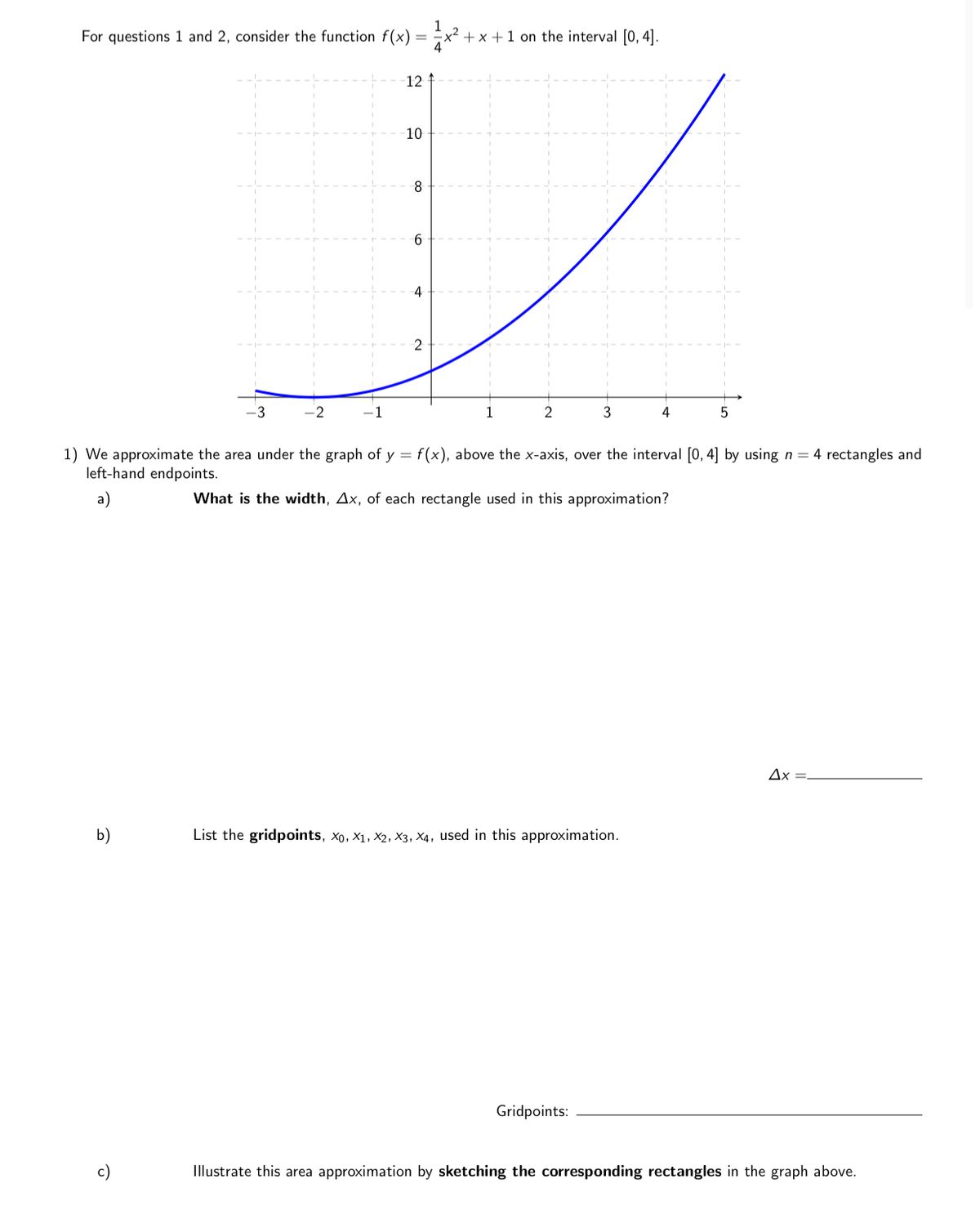



Answered For Questions 1 And 2 Consider The Bartleby
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the intervals in which the function `f` given by f(x) = sin x cos x, 0 `The Mean Value Theorem for Definite Integrals If f ( x) is continuous on the closed interval a, b , then at least one number c exists in the open interval ( a, b) such that The value of f ( c) is called the average or mean value of the function f ( x) on the intervalTranscribed Image Textfrom this Question Find the intervals where f" (x) < 0 ir f" (x) 0 as indicated at I 13) f (x)
Q Determine the average rate of changes in the value of y in moving from x=1 and x=2 f (x) = 5x3 arrow_forward Q Find the average rate of change of f (x)=−x29x on the interval 1,6 arrow_forward Q Find the average rate of change of g (x) = 2x^4 3/x^3 on the interval In a graph of any function, values of f(x) are represented by the values on the yaxis for the different input values on xaxis For the given graph, values of f(x) are less than zero That means interval in which the values of the function are negative for the different values of x Negative values of the given function are in the intervals (∞, 3), (11, 9) Therefore, from theA (24,11) b (3,11) c (11,2) d (11,09)
Answer to Let f (x) = a x^{1 / 2} over the interval 0, 4 and f (x) = 0 for all other values of x (a) For what value of a is f(x) a probability for Teachers for Schools for Working ScholarsWe've already taken definite integrals and we've seen how they represent or they're they denote the area under a function between two points and above the xaxis let's do something interesting let's think about a definite integral of f of X DX so it's the area under the curve f of X but instead of it being between two different X values say a and B like we've seen multiple times let's say it's43 Version 3 Answers 1 Consider the equation below F (x) = 2x^33x^2336x Find the interval on which f is decreasing (Enter your answer in interval notation) Find the local minimum and maximum values of f Find the inflection point Find the interval on which f is concave up



F X 0




Wht Is The Interval Over Which The Function F X 6x X 2 X Gt 0 Is Increasing
Get an answer for '`f(x) = x/(x^2 1)` (a) Find the intervals on which `f` is increasing or decreasing (b) Find the local maximum and minimum values of `f` (c) Find the intervals of concavity Find the value of k, so that the function f defined by f(x) = {kx 1, if x ≤ pi and cos x, if x > pi} is continuous at x = pi asked in Mathematics by Samantha ( 3k points) continuity and differntiabilityNeous rate of change of the function y = f(x) at the point x 0 in its domain is lim x→x0 ∆y ∆x = lim x→x0 f(x 0)−f(x) x 0 −x provided this limit exists Example 1 Let f(x) = 1/x and let's find the instantaneous rate of change of f at x 0 = 2 The first step is to compute the average rate of change over some interval x 0 = 2




Find The Total Area Between The Function F X 2x 2 And The X Axis Over The Interval 9 4 Study Com



Features Of Function Graphs Mathbitsnotebook A1 Ccss Math
2 Answers2 Active Oldest Votes 0 Notice that the graph of f crosses the x axis at − 3, − 2, 0, 2 and 3 Using the fact f ( x) > 0 on the interval where the graph is above the x axis, and f ( x) < 0 on the interval where the graph is below the x axis we have a f ( x) > 0 for x ∈ ( − 3, − 2) ∪ ( 0, 2) ∪ ( 3, ∞)Let F(x)= T Vird Let F(x) = VIt dt over the interval 0, л 2 sinx Which of the following is a FALSE statement?Get an answer for 'Determine the intervals on which the function f(x)=x^x defined on the interval (0,∞) is decreasing and increasing' and find homework help for other Math questions at eNotes



Increasing And Decreasing Functions



Which Expression Can Be Used To Determine The Aver Gauthmath
If f′′(x) > 0 for all x ∈(a,b), then f is concave upward on (a,b) If f′′(x) < 0 for all x ∈(a,b), then f is concave down on (a,b) Defn The point (x0,y0) is an inflection point if f is continuous at x0 and if the concavity changes at x0 Second derivative test If f′′ continuous at c, then If f′(c) = 0 and f′′(c) > 0, then f has a local minimum at cF 4th intervals The Solution below shows the 4th note intervals above note F, and their inversions on the piano, treble clef and bass clef The Lesson steps then explain how to calculate each note interval name, number, spelling and quality The final lesson step explains how to invert each interval For a quick summary of this topic, and to see the important interval table used toIn other words, we may define an improper integral as a limit, taken as one of the limits of integration increases or decreases without bound Definition Let f (x) f (x) be continuous over an interval of the form The Laplace transform of a continuous function over the interval 0,




Analyzing Graphs Flashcards Quizlet



Properties Of Functions Boundless Algebra
Math 151 cBenjamin Aurispa What does f′′ say about f?To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the intervals in which `f(x)=(x1)^3(x2)^2`is increasing or decreasingSal finds the intervals where the function f(x)=x⁶3x⁵ is decreasing by analyzing the intervals where f' is positive or negative If you're seeing this message, it means we're having trouble loading external resources on our website



How To Tell Where F X Is Less Than 0 Or Greater Than 0 Youtube



If F X 0 Over Some Interval Then We Know That F Chegg Com
That would be a gap Now suppose f(x) = 0 if x ∈ A and f(x) = 1 if x ∈ B Then f ′ (x) = 0 for every value of x, but f is not constant You can't prove every function whose derivative is everywhere 0 is constant unless you rule out gaps The proof of the mean value theorem conventionally relies on Rolle's theorem, which in turn relies onIn a graph of any function, values of f(x) are represented by the values on the yaxis for the different input values on xaxis For the given graph, values of f(x) are less than zero That means interval in which the values of the function are negative for the different values of x Negative values of the given function are in the intervals (∞, 3), (11, 9) Therefore, from the givenF(x) < 0 over the interval (–∞, –4) F(x) < 0 over the interval (–∞, –3) F(x) > 0 over




Introduction To Mathematical Modeling Test 1 Form A Solved Math 1101 Docsity



X F X Which Is A Valid Prediction About The Continuous Function F X Course Hero
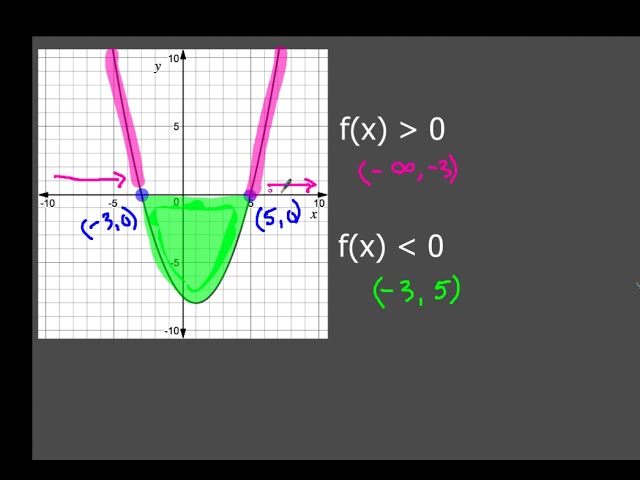
Definition A sequence of functions fn X → Y converges uniformly if for every ϵ > 0 there is an Nϵ ∈ N such that for all n ≥ Nϵ and all x ∈ X one has d(fn(x), f(x)) < ϵ Uniform convergence implies pointwise convergence, but not the other way around For example, the sequence fn(x) = xn from the previous example converges pointwise Answers 1 Get Answers answered bitty3970 f (x) is the same as y, so we can say y = f (x) Writing f (x) < 0 means we want to find when y < 0 Visually, we are looking at the graph when the curve is below the horizontal x axis This is the portion in red that I have marked in the diagram (see attached image below) Answers 2 on a question Analyze the graph of the function f(x) to complete the statement on a coordinate plane, a curved line, labeled f of x, with a minimum value of (0, negative 3) and a maximum value of (negative 24, 17), crosses the xaxis at (negative 3, 0), (negative 11, 0), and (09, 0), and crosses the yaxis at (0, negative 3) f(x)< 0 over (∞,3) and what other interval




Find The Largest And Smallest Values Of The Given Function Over The Prescribed Closed Bounded Interval Of F X 3x 1 E X For X 0 Study Com



Concave Up
And its Fourier series "representation" are only equal to each other if, and whenever, f is continuous integrating over any interval of length 2 L Example Find a Fourier series for f (x) = x, 0 < x < 4, f (x 4) = f (x) How Answers 3, question answers question 1 stepbystep explanation 1/4 of 84 = 84÷4= 21 F(x) on a coordinate plane, a curved line, labeled f of x, with a minimum value of (0, negative 3) and a maximum value of (negative 24, 17), crosses the xaxis at (negative 3, 0), (negative 11, 0), and (09, 0), and crosses the yaxis at (0, negative 3) f(x)< 0 over (∞,3) and what other interval?




Which Statement Is True About The Given Function A F X Gt 0 Over The Interval Infinity 3 B Brainly In




Graph F X 2 Sin X Over The Interval Left 0 2 Pi Right Using The Graph Identify The Absolute Extrema Of The Function If They Exist Study Com
The thin, redshaded area shows just how much difference there is between these two integrals over the interval \(0,1\) Figure \(\PageIndex{9}\) (a) The graph shows that over the interval \(0,1,g(x)≥f(x),\) where equality holds only at the endpoints of the interval (b) Viewing the same graph with a greater zoom shows this more clearlyThe answers to ihomeworkhelperscomDefinitions Probability density function The probability density function of the continuous uniform distribution is = { , < >The values of f(x) at the two boundaries a and b are usually unimportant because they do not alter the values of the integrals of f(x) dx over any interval, nor of x f(x) dx or any higher moment Sometimes they are chosen to be zero, and sometimes chosen to be 1 / b − a
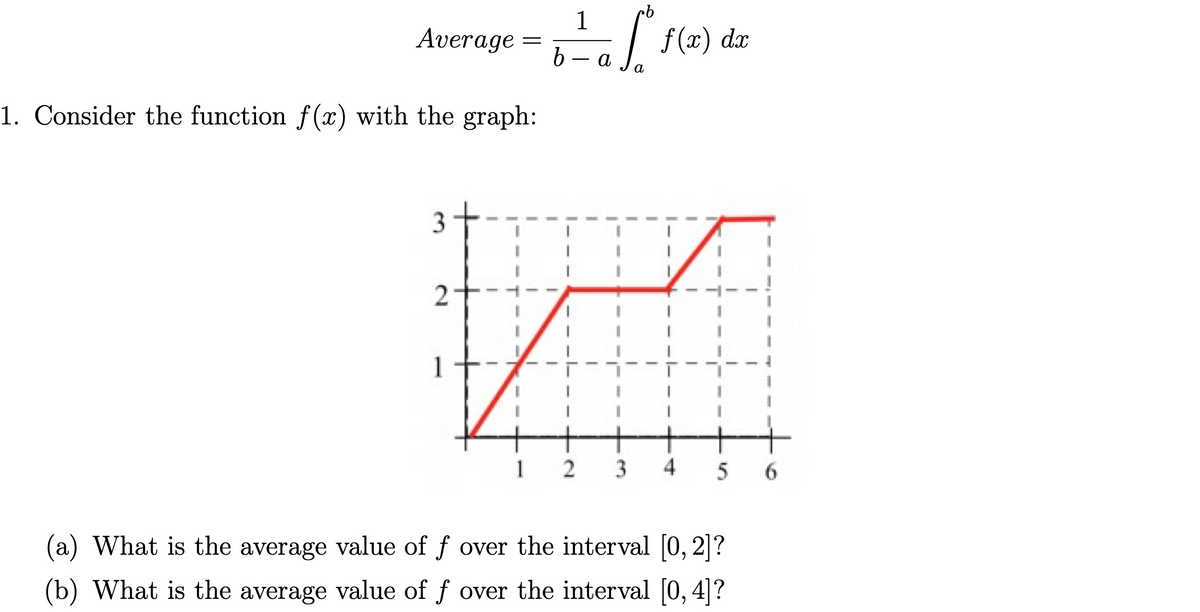



Answered Average F X Dx B A A Consider The Bartleby
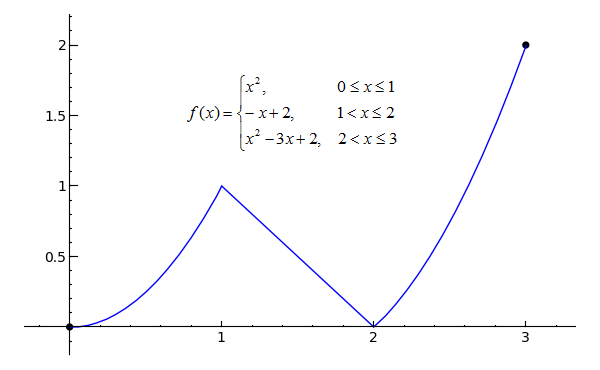



Sage Calculus Tutorial Continuity
We can see from the graph that over the interval 0, 1, g (x) ≥ f (x) 0, 1, g (x) ≥ f (x) Comparing the integrals over the specified interval 0, 1, 0, 1, we also see that ∫ 0 1 g (x) d x ≥ ∫ 0 1 f (x) d x ∫ 0 1 g (x) d x ≥ ∫ 0 1 f (x) d x (Figure 124) The thin, redshaded area shows just how much difference there isSo, suppose we need to find the Fourier series for the function f(x)=x defined on the interval (0,2) How can we do this since this function is not periodic?A F(0)=1 b F"(0) = 0 i Vedi d c lim x10 = 0 dx 12 d None of the other choices is a false statement Question let F(x)= T Vird Let F(x) = VIt dt over the interval 0, л 2 sinx Which of the following is a FALSE statement?




Consider The Function F X Cos X Over The Interval 0 5 Pi 4 Consider The Region R Bounded By The Graph Of F X And The X Axis Over The




Which Statement Is True About The Graphed Function A F X Lt 0 Over The Interval 4 B X Brainly Com
First, as we alluded to in the previous section one possible interpretation of the definite integral is to give the net area between the graph of f(x) and the x axis on the interval a, b So, the net area between the graph of f(x) = x2 1 and the x axis on 0 Transcript Ex 62, 3 Find the intervals in which the function f given by f (𝑥) = sin 𝑥 is (a) strictly increasing in (0 , 𝜋/2) f(𝑥) = sin 𝑥 f'(𝒙) = cos 𝒙 Since cos 𝑥 > 0 for 𝑥 ∈ ("0 , " 𝜋/2) ∴ f'(𝑥) < 0 for 𝑥 ∈ (0 , π) Thus, f is strictly increasing in ("0 , " 𝜋/2) Rough cos 0 = 1 cos 𝜋/4 = 1/√2 cos 𝜋/2 = 0 Value of cos𝑥 > 0 F(x) < 0 over the interval (–∞, –4) F(x) < 0 over the interval (–∞, –3) F(x) > 0 over the interval (–∞, –3) F(x) > 0 over the interval (–∞, –4) Solution f(x) cuts x axis at 4 Hence interval (∞ , 4) and ( 4 , ∞ ) (∞ , 4) f(x) > 0 ( 4 , ∞ ) f(x) < 0



Over What Interval Is The Graph F X X 8 2 Decreasing




Which Statement Is True About The Graphed Function 3 O F X Lt 0 Over The Interval 0 4 O Brainly Com
If \(f'(x)=0\) over an interval \(I\), then \(f\) is constant over \(I\) If two differentiable functions \(f\) and \(g\) satisfy \(f′(x)=g′(x)\) over \(I\), then \(f(x)=g(x)C\) for some constant \(C\) If \(f′(x)>0\) over an interval \(I\), then \(f\) is increasing over \(I\) If \(f′(x)F(x) < 0 over the intervals (∞, 07) and (076, 25) Which statement is true about the end behavior of the graphed function?As the xvalues go to




Ex 6 2 6 Find Intervals In Which Functions Strictly Increasing




Quiz About Derivatives To Analyze Functions Proprofs Quiz




Taylor S Theorem Wikipedia
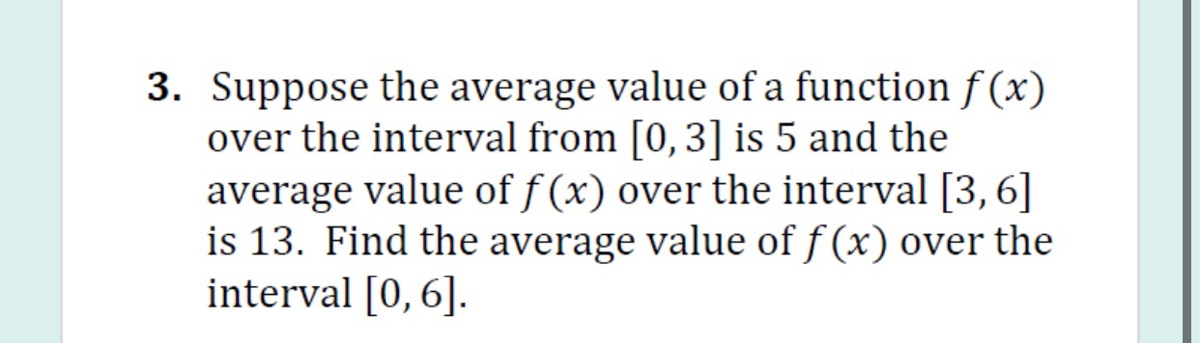



Answered 3 Suppose The Average Value Of A Bartleby
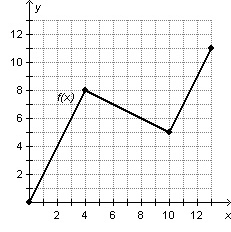



What Is The Average Rate Of Change In F X Over The Interval 4 13 Home Work Help Learn Cbse Forum
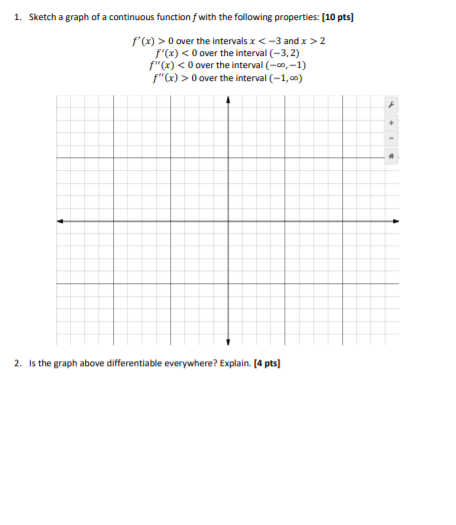



1 Sketch A Graph Of A Continuous Function F With The Chegg Com
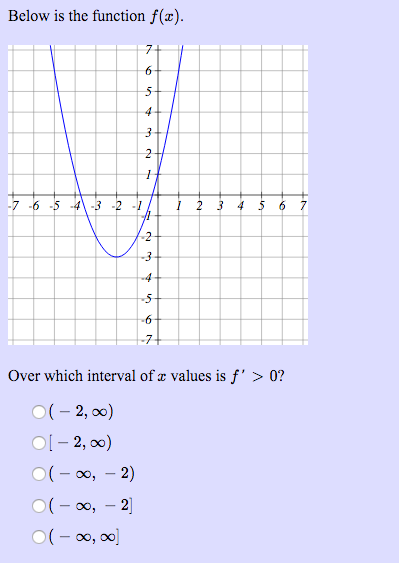



Below Is The Function F X 6 43 2 23 456 5 4 Over Chegg Com



Increasing And Decreasing Functions




Quiz About Derivatives To Analyze Functions Proprofs Quiz




Find The Area Bounded By The Graphs Of The Indicated Equations Over The Given Interval Y X 2 21 Y 0 3 Less Than Or Equal To X Less Than Or Equal To 0 Study Com
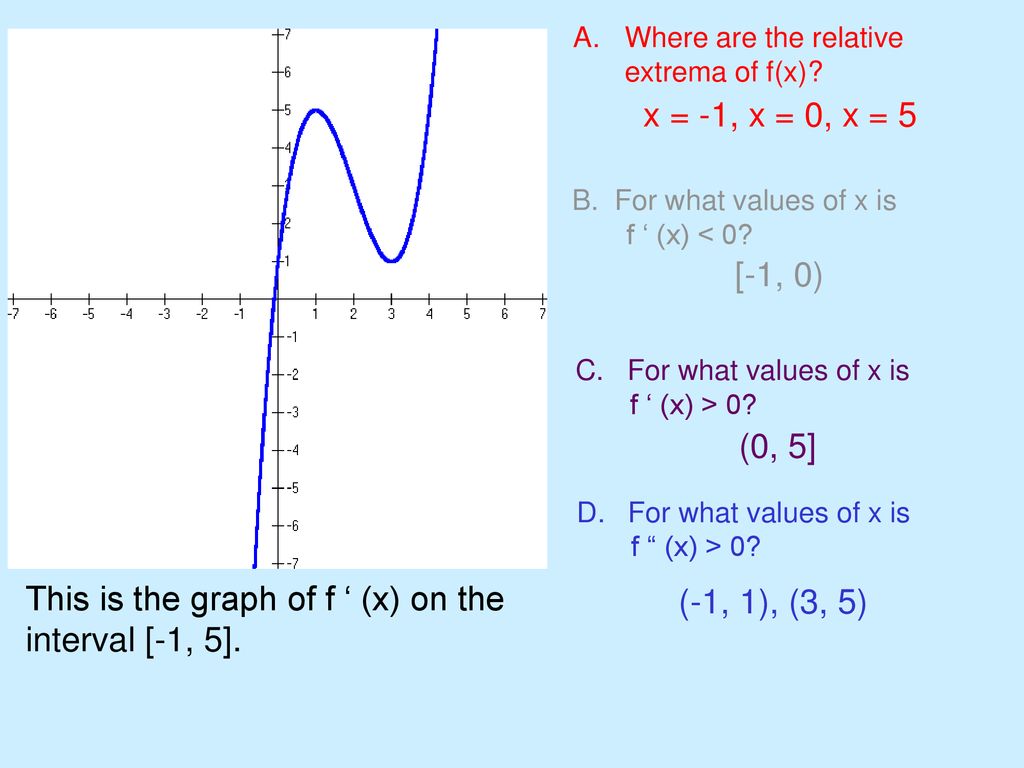



Critical Numbers Relative Maximum And Minimum Points Ppt Download
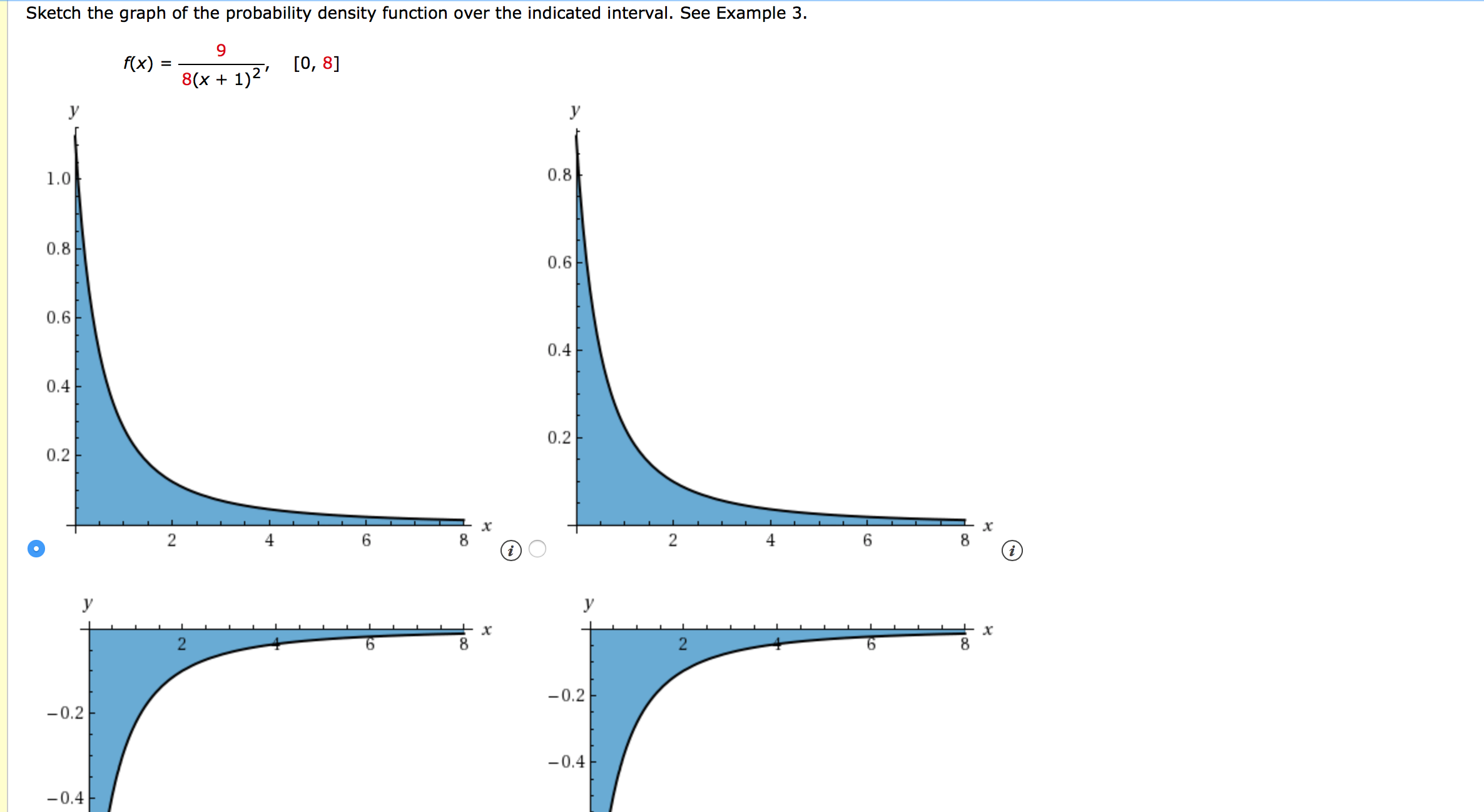



Answered Sketch The Graph Of The Probability Bartleby



Search Q F X 3e0 Tbm Isch




Ex 6 2 19 Mcq The Interval In Which Y X2 E X Is Increasing
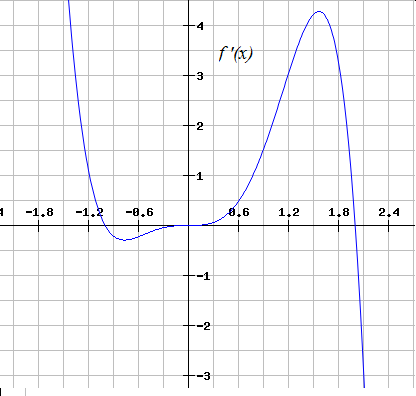



How To Find Increasing Intervals By Graphing Functions Calculus 1
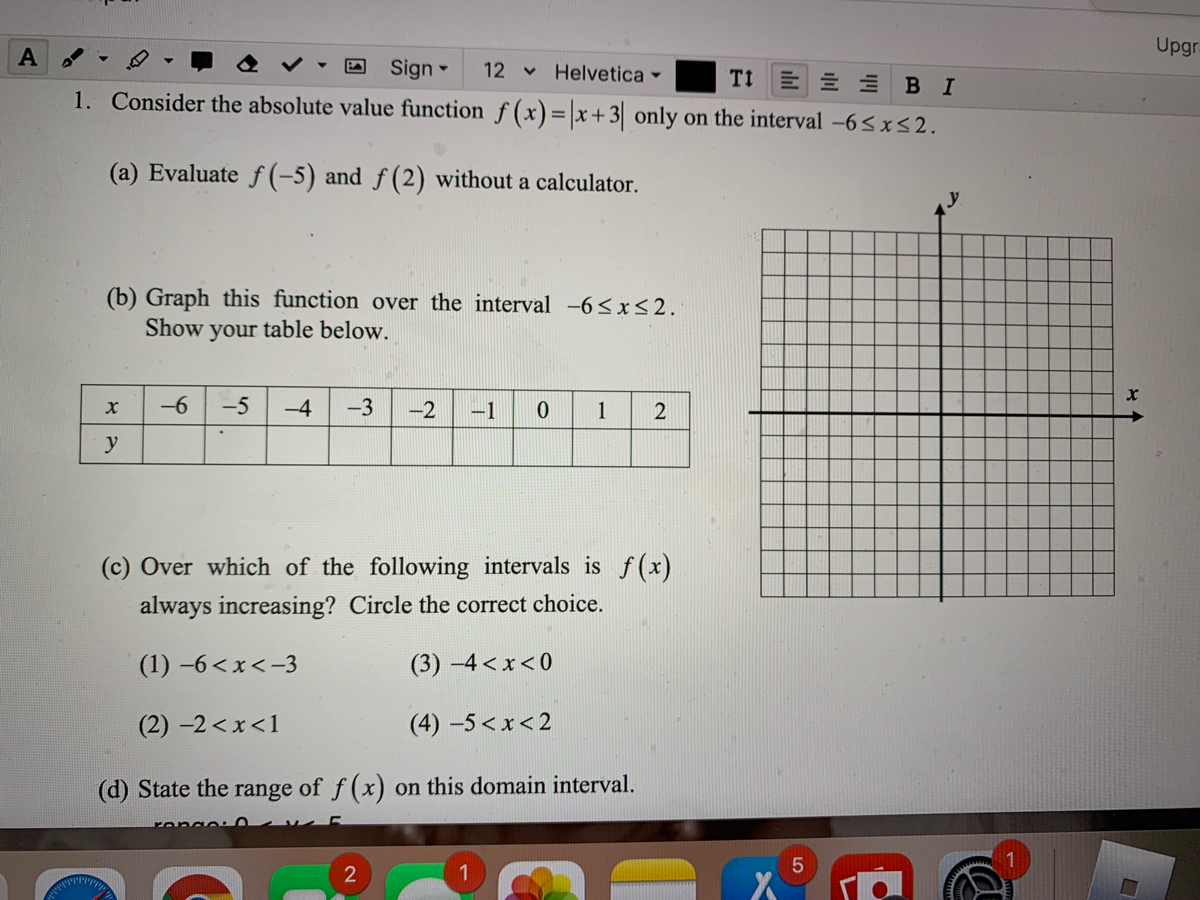



Answered Sign 12 V Helvetica E E E Bi 1 Bartleby




Which Intervals Show F X Increasing Check All That Apply 2 5 1 6 2 1 1 6 0 0 Brainly Com




If F X 0 On An Interval Then F Is Concave Up On Chegg Com
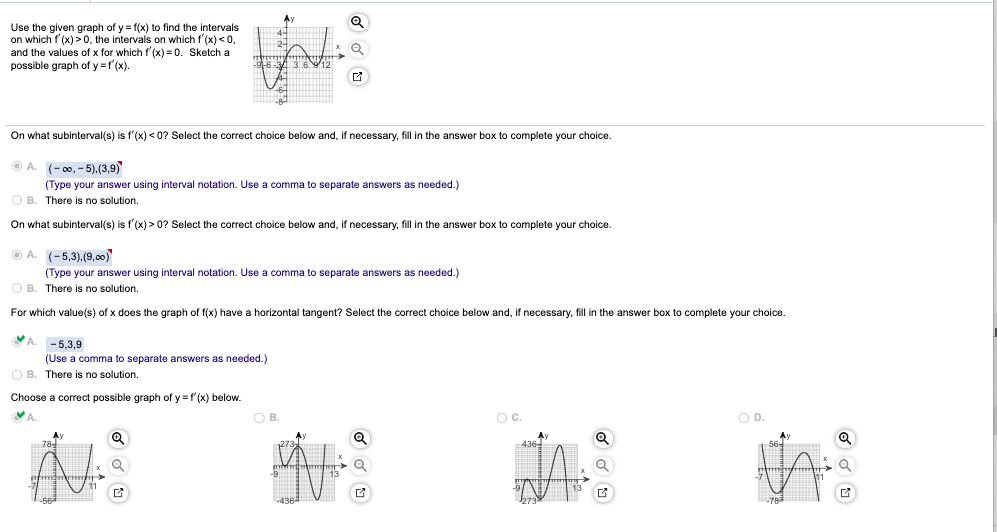



Use The Given Graph Of Y F X To Find The Intervals Chegg Com
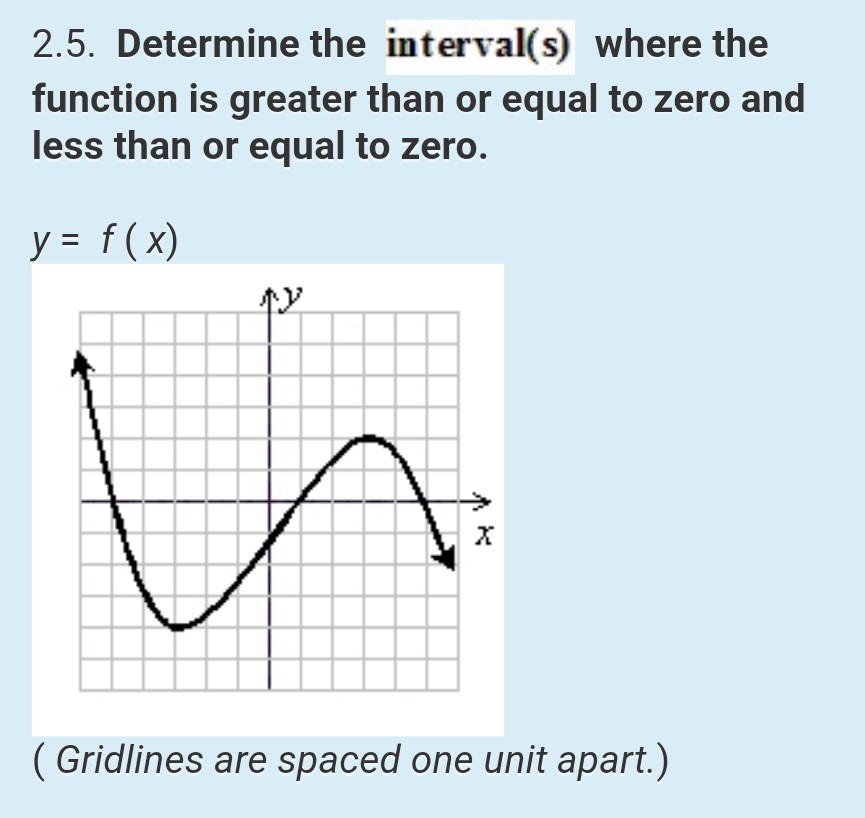



2 5 Determine The Interval S Where The Function Is Chegg Com




How To Use Graph To Determine Where F X 0 And F X 0 Mathematics Stack Exchange




Daily Challenge Please Solve The Following Without A Gdc Ppt Download




Which Statement Is True About The Graphed Function F X 0 Over




Analyzing Graphs Flashcards Quizlet




Determine Whether The Function Shown Is Continuous Over The Interval 5 5 Use The Graph To Answer The Question A Is F Continuous At X 4 B Is F Continuous At X 0 Study Com
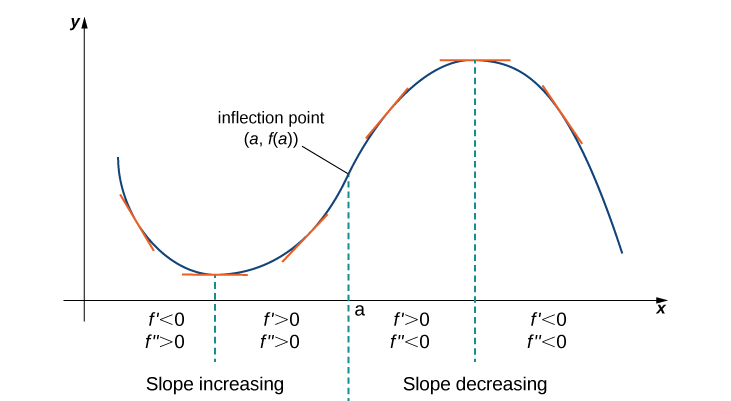



3 5 Derivative Tests Mathematics Libretexts
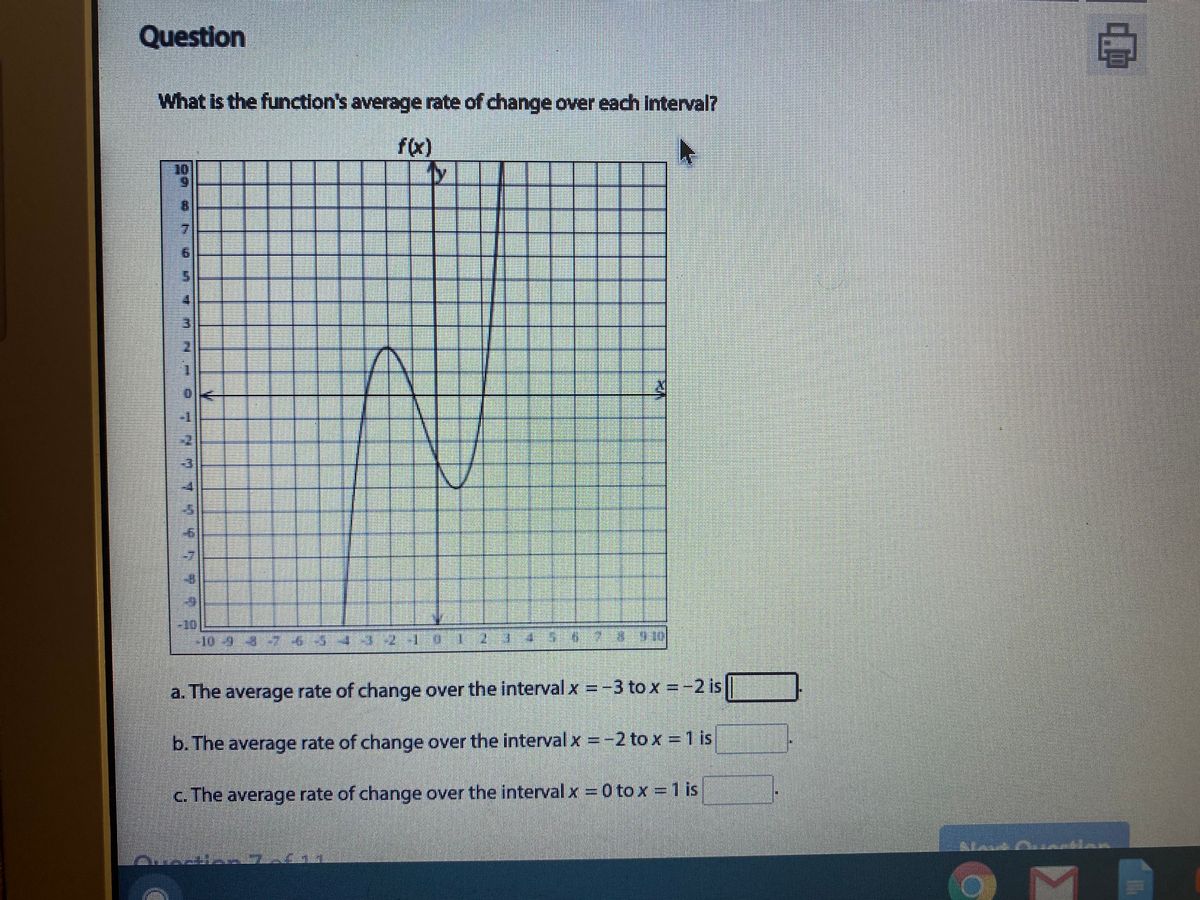



Answered Question What Is The Function S Average Bartleby
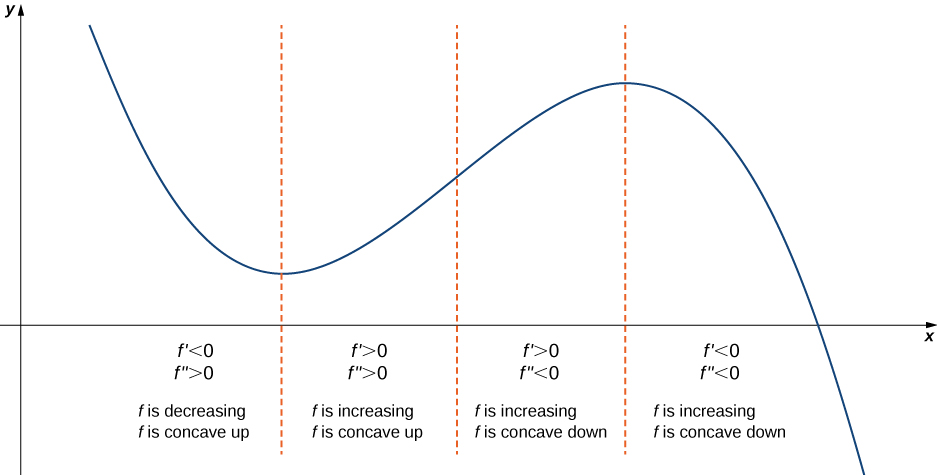



4 3 Derivatives And The Shape Of A Graph Mathematics Libretexts




Average Value Of F X




Which Statement Is True About The Graphed Function F X Lt 0 Over The Interval 4 F X Lt 0 Brainly In




The Graph Of F X The Derivative Of X Is Continuous For All X And Consists Of Five Line Segments As Shown Below Given F 0 6 Find



Plot Expression Or Function Matlab Fplot




Use The Given Graph Of Y F X To Find The Intervals Chegg Com




9 Sketch The Graph Of A Function Using The Given Information A Intercepts 0 0 And 4 0 L Homeworklib



Sage Calculus Tutorial Continuity




Calculate The Average Rate Of Change Of Fx Over Th Gauthmath




Please Follow The Specified Method Solve For X 4sin 2x Scos X 0 Over Homeworklib




Which Statement Is True About The Graphed Function F X Lt 0 Over The Intervals 0 7 And Brainly Com




Use The Graph Of F To Determine Where A F X 0 And Chegg Com
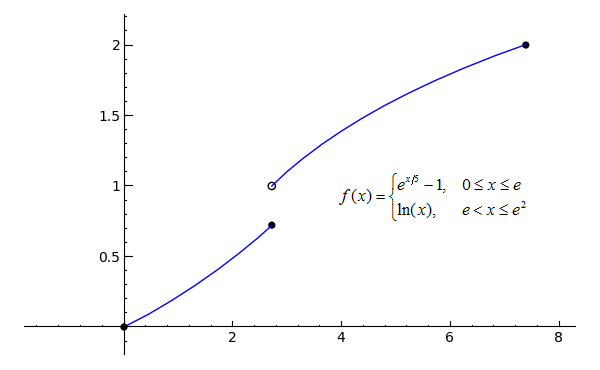



Sage Calculus Tutorial Continuity




Pdf Optimal Piecewise Linear Function Approximation For Gpu Based Applications




Lesson Explainer Concavity And Points Of Inflection Nagwa




Use A Graph To Determine Where A Function Is Increasing Decreasing Or Constant College Algebra




Which Statement Is True About The Given Function A F X 0 Over The Intervals Infinity 2 7 And 0 8 Infinity B F X 0 Over The Intervals Infinity 2 7 And 1 0 8
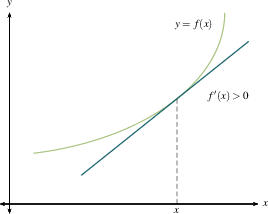



F Vs F
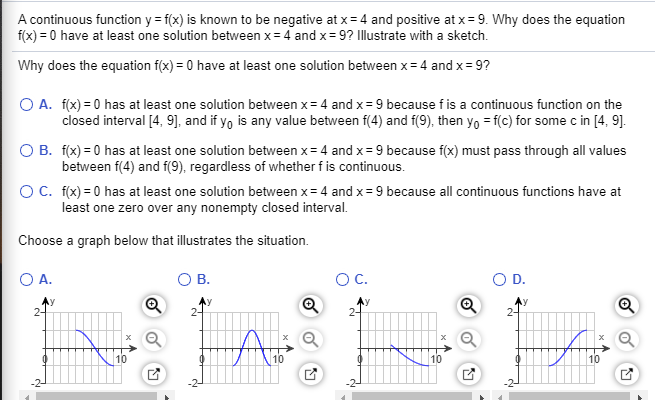



Answered A Continuous Function Y F X Is Known Bartleby
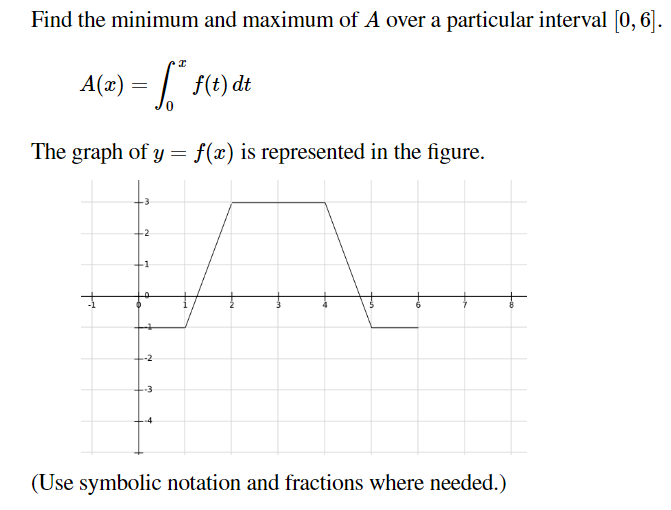



Answered Find The Minimum And Maximum Of A Over Bartleby




Answered For Questions 1 And 2 Consider The Bartleby
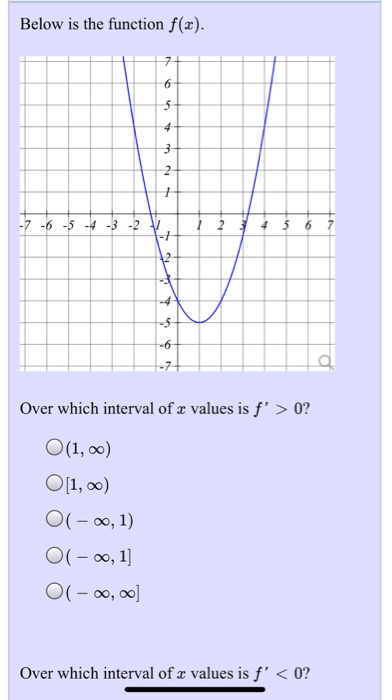



Below Is The Function F X 7 6 5 4 3 2 V 2 4 5 Chegg Com
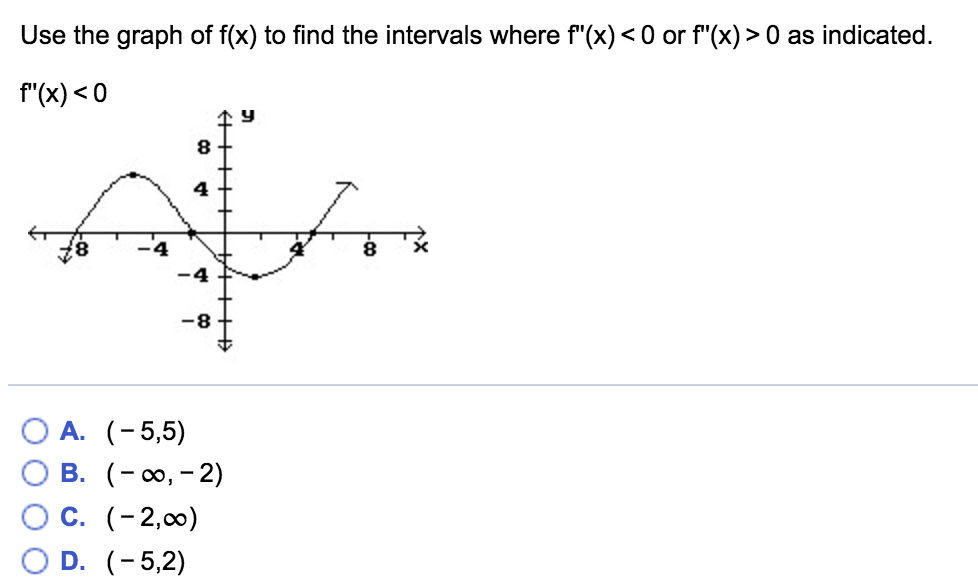



Use The Graph Of F X To Find The Intervals Where Chegg Com




F X Lt 0 Over 3 And What Other Interval O 2 4 1 1 O 3 1 1 O 1 1 2 O 1 1 Brainly Com
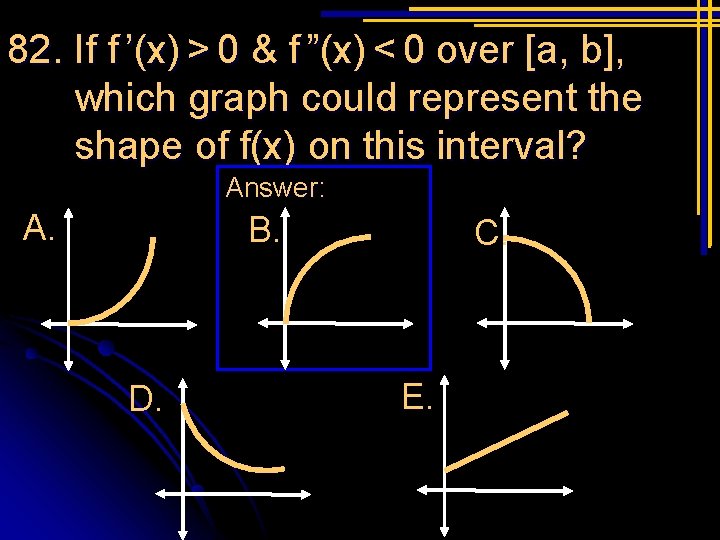



Ap Exam Review Competition First To Finish Calls




Analyzing Graphs Flashcards Quizlet
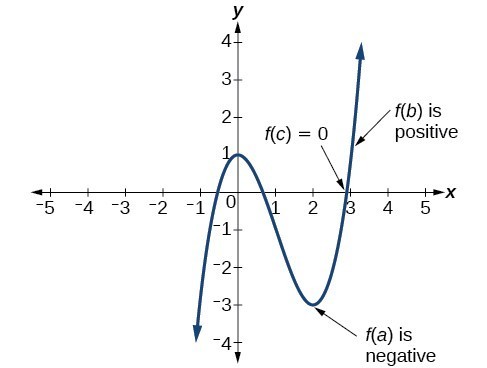



Use The Intermediate Value Theorem College Algebra
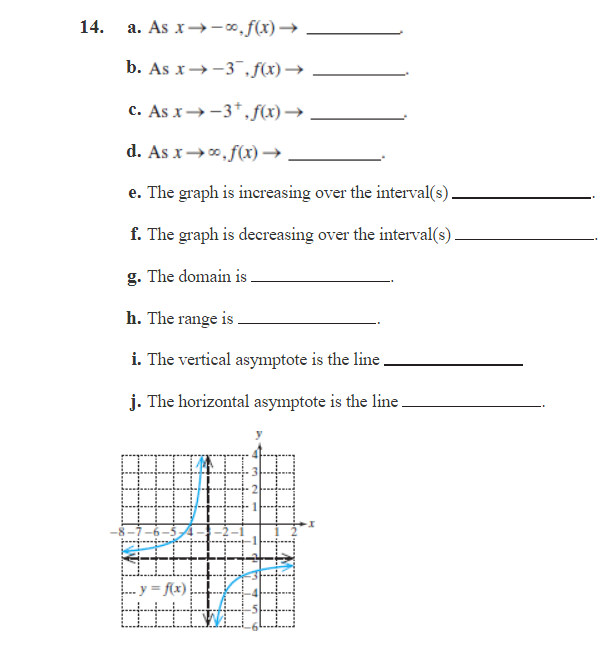



Answered 14 A As X 0 F X B As X 3 Fx C Bartleby
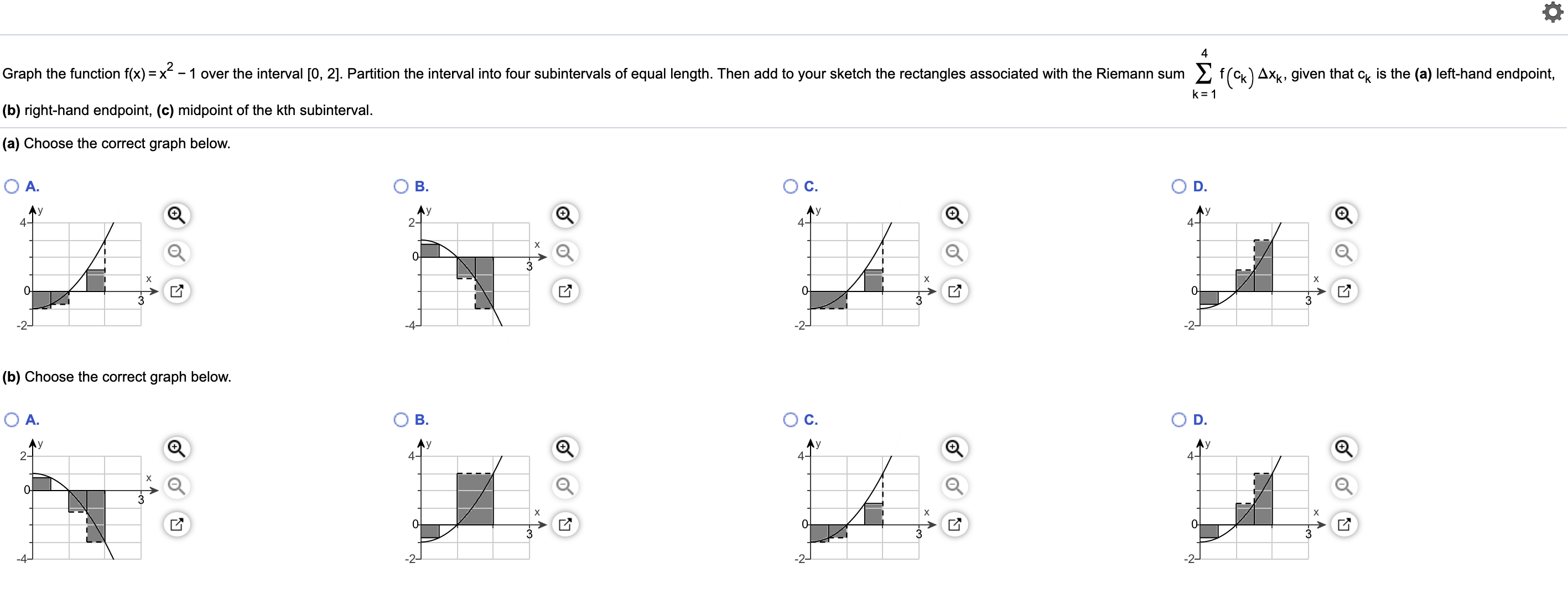



Answered C Choose The Correct Graph Below A Bartleby




There Is An Area A Bounded By The Curve Fx X2 And Gauthmath




Finding Average Rate Of Change Of Polynomials Video Khan Academy
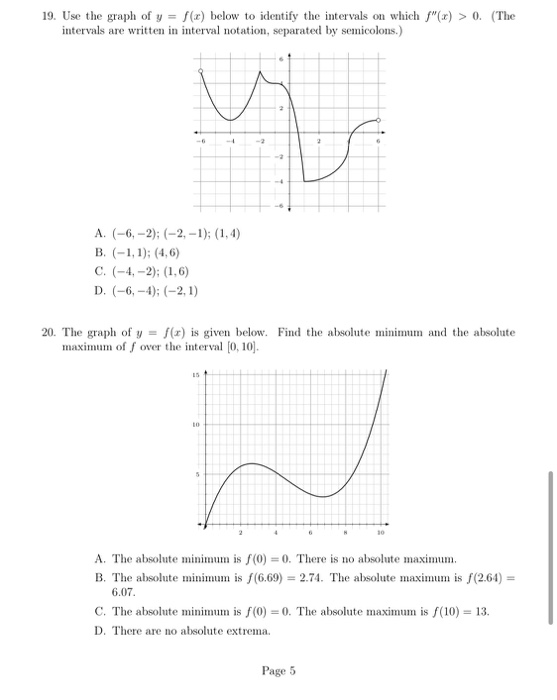



19 Use The Graph Of Y F X Below To Identify The Chegg Com



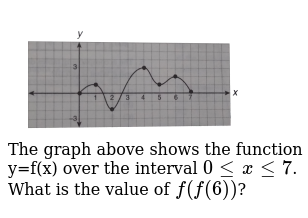
1




Which Is A Valid Prediction About The Continuous F Gauthmath
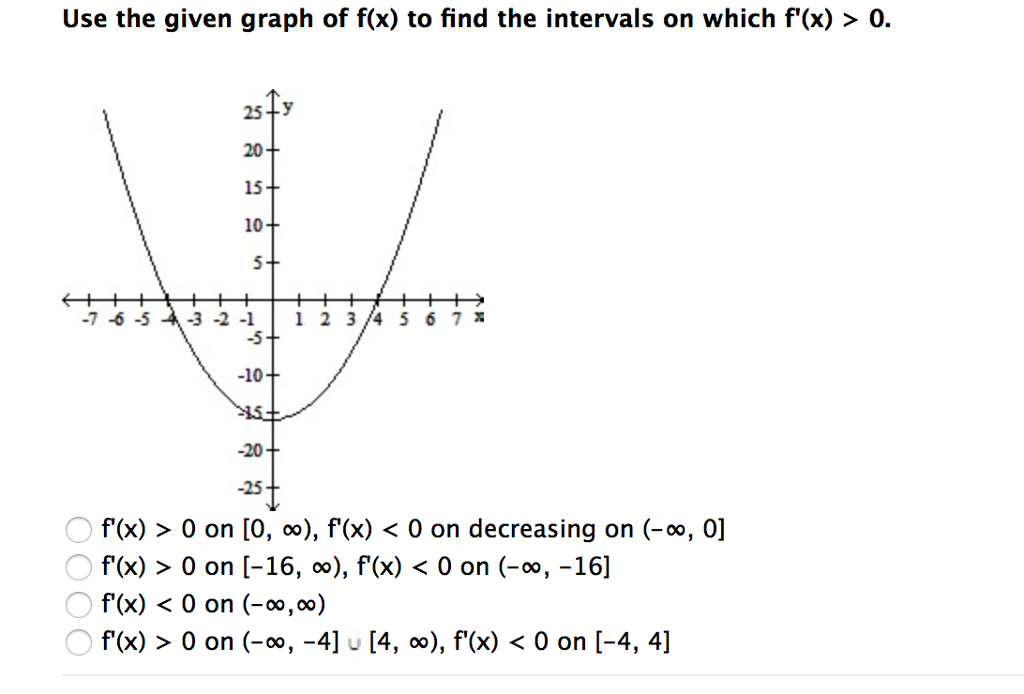



Use The Given Graph Of F X To Find The Intervals On Chegg Com




Differential Calculus Sketching The Graph Of F Given Info About F And F Youtube
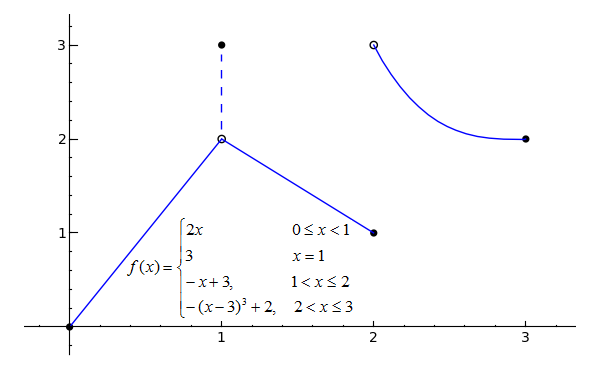



Sage Calculus Tutorial Continuity




5 Consider The Function Fx Cube Root Ofx 1 2 Ov Gauthmath




Intermediate Value Theorem Wikipedia



Diracc Sec 8 2




Which Statement Is True About The Graphed Function F X Lt 0 Over The Interval 4 F X Lt Brainly Com



If X Belongs To 0 2p Then At What Interval Is F X Cosx Decreasing Quora




Continuity Over An Interval Video Khan Academy
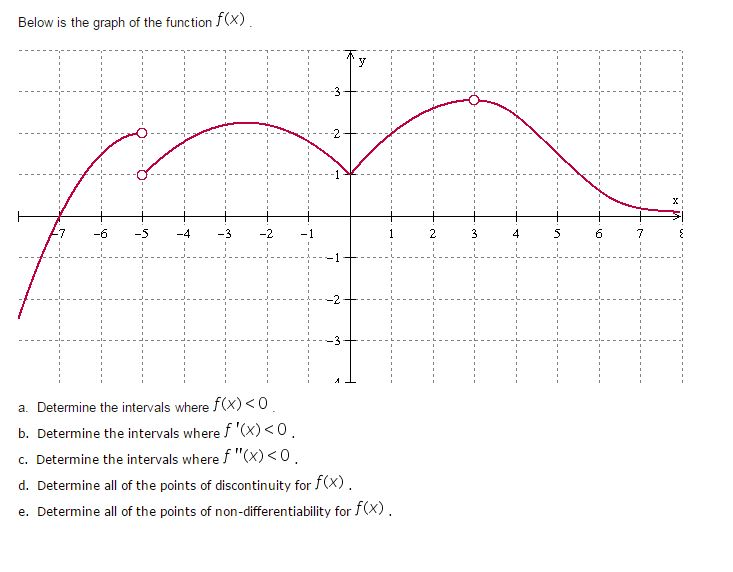



Below Is The Graph Of The Function F X Determine Chegg Com
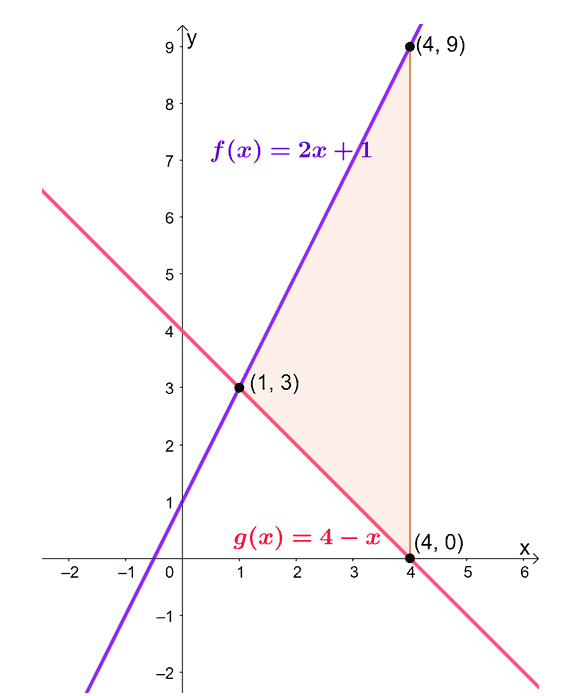



Area Between Two Curves Definition Process And Examples



Web Viu Ca Pughg Summer12 Math121m12n01 Secondderivativenotes Pdf




Analyzing Tables Flashcards Quizlet




Question Video Find The Absolute Maximum And Minimum Of A Piecewise Defined Function Nagwa



If A Function Is Defined By F X X X How Do You Find The Average Rate Of Change Of Y With Respect To X Over The Interval 1 3 And The Instantaneous




Legendre Polynomials Wikipedia




Test Analyzing Tables Quizlet
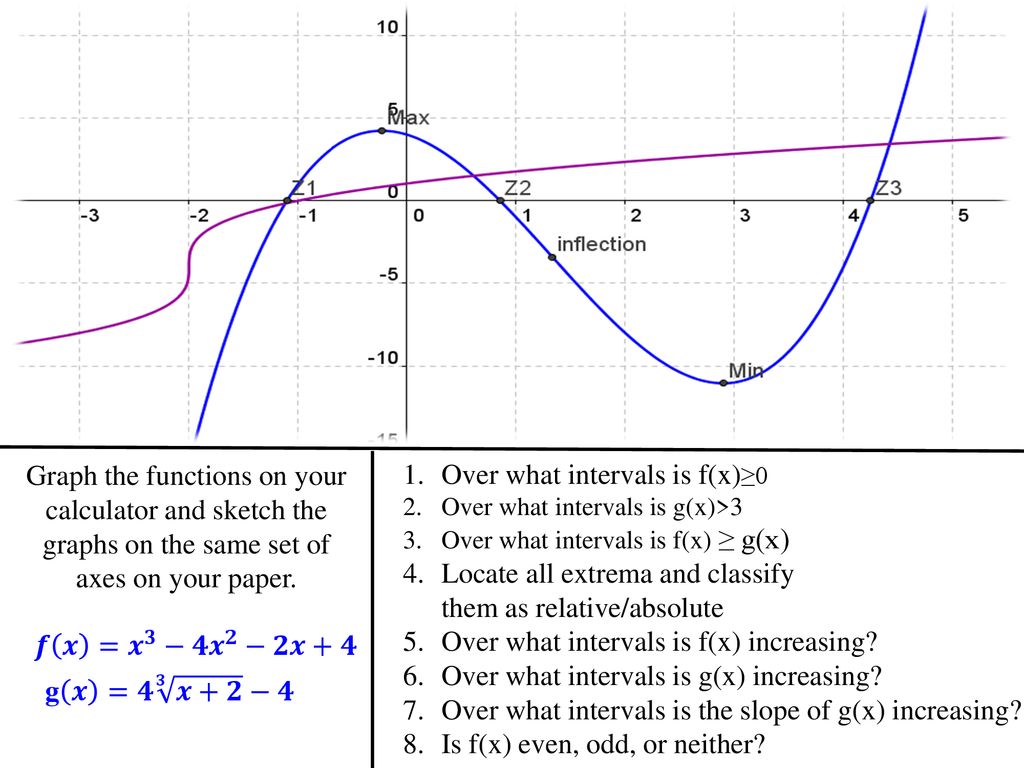



Functions Change Lesson Section Ppt Download



Derivatives And The Shape Of A Graph Calculus



2 4 Continuity Calculus Volume 1




Left A Solution Trajectory Of System X F X With F From 1 Download Scientific Diagram



No comments:
Post a Comment